Возможные ошибки и основные показатели точности опытов
Даже при самой тщательной работе урожаи на параллельных делянках и в параллельных сосудах получаются не совсем одинаковыми.
Расхождение между урожаями в параллельных сосудах или на параллельных делянках будет характеризовать степень точности нашей работы. Если бы в нашем опыте не было грубых или систематических ошибок, то при громадном числе параллельных делянок или сосудов среднее арифметическое соответствовало бы истинному урожаю, который мы должны были бы получить при точном выполнении всех операций.
Если для той или другой делянки или для того или другого сосуда была допущена грубая ошибка, т. е. нарушено правило постановки опыта, то урожаи этих делянок и сосудов выбраковывают и не учитывают при суммировании урожаев параллельных делянок или сосудов и выведении средних урожаев по вариантам опыта.
Под систематическими ошибками понимаются такие недостатки в постановке опыта, которые вызывают закономерные, идущие в определенном направлении, изменения урожаев по повторностям опыта. При помощи статистической обработки полученных величин иногда удается выявить наличие в опыте систематической ошибки и внести соответствующие исправления в подсчеты его результатов. В вегетационных опытах, как правило, систематических ошибок не должно быть; в полевых опытах они часто вызываются различным плодородием опытного участка. Если изменения почвенного плодородия опытного участка происходят в определенном направлении (например, постепенное изменение плодородия почвы при постановке опыта вдоль склона), то эти изменения можно выявить и до некоторой степени устранить их влияние на статистическую обработку результатов опыта.
Статистическая обработка результатов опыта позволяет установить точность опыта, а в некоторых случаях внести исправления и в самые подсчеты результатов опыта, например, в тех случаях, когда вводится поправка на систематическую ошибку опыта или производится выбраковка делянок или сосудов, для которых была допущена грубая ошибка, оставшаяся не отмеченной в журнале опыта.
Исходная предпосылка при обработке результатов опытов — предположение, что когда нет грубых и систематических ошибок, то урожаи параллельных делянок или сосудов располагаются определенным образом вокруг истинной величины урожая для данного варианта, образуя, при громадном числе параллельных показаний, кривую нормального распределения показаний, и что среднее арифметическое из всех параллельных урожаев соответствует истинному значению урожая для данного варианта. Так как мы не можем ставить большого числа параллельных опытов для каждого варианта, то наши средние арифметические полученных урожаев не являются точными показателями истинного урожая для данного варианта. Ho зная, что отдельные показания определенным образом располагаются вокруг истинного среднего, мы можем установить, какова вероятность отклонения эмпирической средней на ту или другую величину от истинного результата.
Изучением этого вопроса занимается вариационная статистика; ниже приведем из нее тот минимум сведений, который необходим для обработки результатов нормально проведенного опыта, чтобы установить степень его точности.
На рисунке представлена кривая нормального распределения показаний при бесконечно большом числе параллельных определений (кривая Гаусса). На горизонтальной линии (на оси абсцисс) в обе стороны от точки М, соответствующей средней арифметической, отложены величины отклонений от нее отдельных показаний. Как видно из рисунка, больше всего показаний располагается вблизи среднего арифметического — над точкой M кривая имеет выпуклую форму, которая потом переходит в вогнутую. Следовательно, по мере увеличения отклонения от среднего число показаний, сильно разнящихся от среднего, становится все меньше. Точка перегиба кривой, где она переходит из выпуклой в вогнутую, соответствует так называемому квадратическому основному отклонению, обозначаемому греческой буквой а.
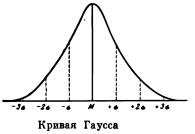
Число показаний, которые отклоняются от среднего арифметического больше чем на ± σ, равно трети общего числа показаний. Отклонения больше чем на ± 2 σ имеют место только для 1/22 всех определений, а отклонение их от среднего больше чем на ±3 σ встречается только один раз из 370 случаев. Если бы нам удалось определить основное отклонение для полученных в нашем опыте результатов, то мы узнали бы и точность нашего опыта, т. е. могли бы сказать, какова вероятность того, что наши показания отклонились от истинного результата на ту или другую величину. Например, если основное отклонение в нашем опыте было равно ± 0,5 ц, то урожаи отдельных делянок могут отклониться от истинного среднего для данного варианта на ± 1,5 ц только 1 раз из 370 возможных случаев.
В опытах мы применяем два и больше повторений и берем среднее из них. В этом случае достоверность нашего определения возрастает пропорционально корню квадратному из числа повторений. Характер распределения наших эмпирических средних вокруг истинного среднего остается тем же, что и распределение вокруг него отдельных показаний, но кривая сжимается около точки М, так как величина основного отклонения σ становится меньше.
Квадратическое отклонение среднего называемся квадратической ошибкой и обозначается буквой m
m = σ/√n,
где n — число параллельных делянок или сосудов, т. е. повторений опыта.
Например, если опыт ставится в четырехкратной повторности, то точность его возрастает в 2 раза (√4) по сравнению с достоверностью опыта с однократной повторностью.
Так как величина основного отклонения вычисляется путем определения отклонений отдельных показаний от среднего арифметического, то установить величину основного отклонения в опыте можно только при наличии в нем минимум двукратной повторности. Поэтому для опыта без повторения вообще нельзя иметь представление о степени его точности и ставить такие опыты как в стационарных, так и в производственных условиях в подавляющем большинстве случаев нецелесообразно.
В опытах нам не столько приходится показывать абсолютную величину тех или других урожаев, сколько сравнивать между собой средние арифметические для различных вариантов опыта. Следовательно, нам надо определить достоверность разности средних арифметических. Если ошибка среднего M1 равна ± m1, а ошибка другого среднего M2 равна ± m2, то ошибка разности (т.D) средних M1 — M2 равна:
т. е. она больше, чем ошибка одного среднего. В большинстве случаев ошибка средних вычисляется сразу для опыта в целом, поэтому m1 = m2 и ошибка разности средних становится ошибкой опыта; следовательно,
В том случае, когда определяется ошибка разности двух средних величин, характеризующих явления, имеющие между собой определенное соотношение, ошибка разности средних для таких сопряженных рядов определяется по формуле
где r — коэффициент корреляции, показывающий степень сопряженности сравниваемых явлений, например изменения плодородия почвы в зависимости от рельефа.
Способы определения величин σ, m и r (табл. 1). Вычисление величины основного, или квадратического, отклонения отдельного определения производится по формуле
где v — отклонение отдельного определения от среднего арифметического; ∑v2 — сумма квадратов отклонений.
Понятно, что соответствующая формула для ошибки среднего будет:
Точность вычисления ошибки зависит от числа определений, использованных для ее вычисления; считают, что ошибка вычисления квадратического отклонения равна σ/√2n, т. е. при восьми показаниях она равна σ/√16= 0,25σ, для нашего примера σ = ±0,66 ± 0,17.
При обычных вычислениях, если определения производились с точностью до 0,01, отклонения от среднего вычисляются с точностью до 0,1 г, а квадраты — с точностью до 0,01.
Вычисление коэффициента корреляции производится по формуле
или по формуле
Ошибка коэффициента корреляции вычисляется по формуле
Величина коэффициента корреляции изменяется от +1 до -1. Когда корреляция отсутствует, коэффициент равен нулю. Когда изменение показаний одного ряда строго соответствует изменению показаний другого ряда, имеем коэффициент +1, или полную положительную связь между явлениями. Если показания одного ряда всегда уменьшаются, а показания другого ряда увеличиваются, имеем обратную корреляцию между явлениями и отрицательный коэффициент корреляции.
Пример вычисления коэффициента корреляции.
В опыте на Краснокутской опытной станции наблюдалась определенная зависимость между урожаем пшеницы и плотностью колоса для различных сортов (табл. 2).
Вычисляем отклонения от средних, перемножаем их попарно и суммируем, получаем ∑v1v2. Возводим отклонения в квадрат и находим ∑v1в2 и ∑v2в2 и (табл. 3).
Таким образом, в этом опыте наблюдалась вполне доказуемая и весьма высокая обратная зависимость между плотностью зерна и урожаем пшеницы.
Коэффициент корреляции показывает только наличие совпадения или расхождения между изменениями, происходящими в двух рядах различных признаков изучаемых объектов, например: плотности колоса у пшеницы и ее урожайности или действия фосфорного удобрения и содержания в почве растворимых фосфатов. Ho коэффициент корреляции не дает представления ч) количественной зависимости между изменениями в двух рядах, т. е. о том, какое изменение плотности колоса дает какую прибавку урожая зерна или при каком уменьшении содержания в почве растворимых фосфатов наблюдается увеличение урожая на 1 ц зерна от внесения фосфорных удобрений.

Меру изменения показаний в одном ряду в соответствии с изменением показаний в другом дает коэффициент регрессии. Он является константой, которая показывает функциональную зависимость между двумя явлениями. Если изменения одного ряда будем рассматривать как изменения независимой переменной, то изменения другого ряда можно считать функцией изменений первого или зависимой от него переменной величиной. Самым простым выражением функциональной зависимости будет уравнение прямой линии:
у = bх,
в котором х — независимая переменная; у — функция от х; b — константа, которая и является коэффициентом регрессии.
Если M1 — среднее для первого ряда показаний, a M2 — для второго, то имеем следующее уравнение:
v2 — М2 = b (v1 — M1),
т.e. b (коэффициент регрессии) показывает, во сколько раз отклонение (v2) от среднего для второго ряда больше или меньше соответствующего отклонения от среднего (v1) в первом ряду. Конечно, этот коэффициент соответствует только простейшему виду функциональной зависимости или прямолинейной регрессии:
у = а + bх.
Возможны более сложные зависимости:
у = a + bx + cx2,
у = abx.
Последняя распространена в биологических явлениях, при вычислениях обычно ее применяют в логарифмической форме, когда она получает вид прямолинейной регрессии:
lg y = lg a + lg b,
Коэффициент прямолинейной регрессии определяется по формуле
b = ∑v1v2/∑v1в2.
Порядок вычисления этого коэффициента регрессии приводится далее. Способы вычисления криволинейной регрессии и множественной регрессии, когда изменение одного признака зависит от изменения двух других признаков, можно найти в руководстве Д.У. Снедекора, где имеется много примеров вычисления коэффициентов корреляции и регрессии из практики агрономических исследований.