Оценка точности опыта
Статистическую обработку результатов опыта производят для установления точности опыта. Ошибка среднего арифметического показывает, с какой степенью точности мы можем судить по величине найденного в опыте среднего о величине того истинного среднего, которое было бы получено в результате суммирования бесконечно большого числа параллельных определений. Согласно кривой нормального распределения всех возможных случаев, можно утверждать, что истинное среднее будет находиться в промежутке между М + m и М — m в 68,3% всех возможных случаев, в промежутке между M + 3m и M — 3m в 99,73% всех возможных случаев, или, говоря другими словами, мы имеем 9973 шанса из 10 000 за то, что наше среднее не отклоняется от истинного больше чем на ± 3 т. Например, если для урожая по NPK мы получили средний урожай в 45,7 ц, а ошибка среднего была 0,6 ц, то истинный урожай по NPK с достоверностью в 99,73% не разнится от 45,7 больше чем на ±3 m = ±1,8 ц. Следовательно, наш вывод, что истинный урожай по NPK, который мы получили бы при большом числе повторений, находится в пределах M ± 3m = 45,7 ± 1,8, или, что то же, в промежутке между 43,9—47,5 ц, имеет большую достоверность. Наоборот, если бы мы стали считать, что истинное значение находится в пределах M ± т = 45,7 ± 0,6, или между 45,1 и 46,3 ц, то в 31,7% всех случаев наше суждение было бы ошибочно. Следовательно, чем больше будет допускаемый нами возможный размер отклонения от среднего, тем достовернее будет наше суждение. Степень же точности нашего определения среднего будет зависеть от величины ошибки среднего. Если бы в нашем опыте ошибка среднего была равна ± 0,1 ц, то в пределах 45,4—46,0 ц находилось бы 9973 из 10 000 возможных случаев. Таким образом, степень точности нашего опыта зависит от величины ошибки среднего, а достоверность наших суждений — от того, во сколько принятый нами размер возможного отклонения истинного результата от среднего будет превышать ошибку последнего. Обычно считают, что истинный результат достаточно точно характеризуется промежутком M ± 3 m (тройная ошибка называется иногда предельной ошибкой среднего). Число, показывающее, во сколько раз установленный предел отклонения от среднего больше его ошибки, обозначается буквой t; чем больше t, тем достовернее наше суждение. В табл. 12 показана зависимость достоверности наших суждений от принятого при анализе результатов предельного отклонения от среднего, выраженного в частях т.
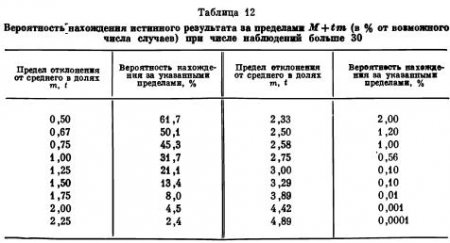
В большинстве опытов приходится не столько устанавливать абсолютные размеры урожая по тому или другому варианту опыта, сколько определять достоверность разности между средними для различных вариантов. Достоверность разности между двумя средними определяется величиной t, которая показывает, во сколько раз разность больше своей ошибки. Обозначая разность через D, имеем:
t = D/mD.
Когда ошибка разности равна самой разности, истинное значение разности между двумя средними, согласно кривой нормального распределения показаний, выйдет за пределы D ± mD в 31,7% всех возможных случаев, так как ошибка разности так же характеризует ее, как обычная ошибка среднего — свое среднее арифметическое. Ho в одной половине возможных случаев истинное значение будет больше нашей эмпирической разности, а в другой половине — меньше. Если речь идет о достоверности разности между средними, т. е. ставится вопрос только о том, действительно ли урожаи по обоим сравниваемым вариантам отличаются друг от друга, то для характеристики достоверности разности имеют значение отклонения только в одном направлении — уменьшения разности между средними.
Предположим, что M1-M2 = mD, т. е. разность равна ошибке разности, t = D/mD — 1; тогда (по табл. 13) 31,7% всех случаев будет находиться за пределами D ± mD, но только в половине из них (15,9%) разность между средними исчезнет или станет обратной. Следовательно, достоверность разности можно характеризовать не 68,3%, а 84,1%, так как в 84,1% всех возможных случаев M1 будет больше, чем M2. В табл. 13 приведены соответствующие данные достоверности разности средних; их легко можно вывести из табл. 12, если учесть, что в данном случае имеет значение только одностороннее отклонение от среднего. Из табл. 12 видно, что если разность более чем вдвое превосходит свою ошибку, то по своей достоверности она уже заслуживает внимания, поэтому в полевых и вегетационных опытах обычно довольствуются двойной ошибкой разности средних в качестве показателя достоверности суждений, имея 95% вероятности, которая получается при t =1,64 mD.
Таблица Стюдента и Фишера. Для оценки достоверности результатов опыта мы можем пользоваться табл. 12 и 13 только в тех случаях, когда ошибка опыта, или среднего арифметического, вычислена на основе обработки сравнительно большого числа данных, т. е. когда в опыте было более 30 делянок или сосудов и применялся обобщенный метод обработки результатов опыта. Если в опыте было небольшое число делянок или производилось вычисление ошибки среднего для каждого варианта опыта в отдельности, то следует пользоваться табл. 14, составленной Стюдентом и несколько видоизмененной Фишером. В этой таблице вероятность нахождения истинного результата в пределах M ± т поставлена в зависимость от числа наблюдений. В первом вертикальном столбце приведено число так называемых степеней свободы, равное для среднего арифметического п — 1, т. е. числу показаний урожаев делянок или сосудов, из которого выведено среднее, уменьшенному на единицу (так как, зная n — 1 показаний, последнее показание можно установить по разности, если известно среднее). В верхнем горизонтальном ряду указана вероятность (в процентах) нахождения истинного результата за пределами M ± tm. В средней части таблицы приведены величины t — коэффициенты, показывающие, во сколько раз принятое при анализе результатов опыта отклонение от среднего больше его ошибки. Например, если мы имеем средний урожай для четырех делянок (n = 4), равный 34,5 ц, и ошибка среднего ±1,1 ц, то вероятность нахождения истинного результата за пределами M ± 3m (что соответствует значению t = 3), т. е. иначе в промежутке от 31,2 до 37,8 ц, будет, как показывает табл. 14, около 5% (в таблице имеем для n — 1 = 3 значение t, близкое к 3, именно 3,18).
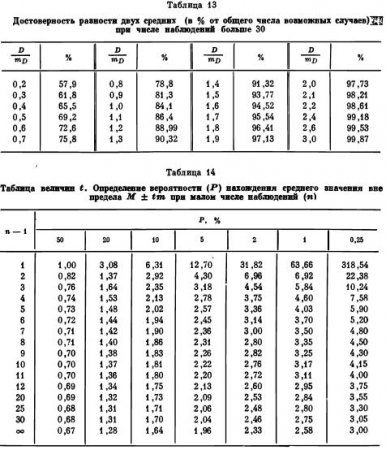
Если бы ошибка среднего была установлена на основе большого числа определений, то вероятность отклонения истинного результата за пределы M ± 3m была бы равна только 0,27 %. Чтобы иметь подобную достоверность наших суждений при n = 4, нам надо размах возможных колебаний среднего принять в M ± 10,24 m, или 34,5 ± 11,3 ц, так как вероятности в 0,27% при n — 1 = 3 соответствует t = 10,24. Таким образом, при четырехкратной повторности так называемая предельная ошибка среднего (т. е. ошибка при t — 3) должна быть принята равной не тройной ошибке, а десятикратной.
Этой же табл. 14 можно пользоваться и для установления достоверности разности между средними M1-M2, т. е. для определения того, во скольких случаях из всех возможных M1 будет больше M2.
В данном случае имеют значение отклонения только в одну сторону, направленные к уменьшению разности между M1 и M2. При отклонении только в одну сторону, положительную или отрицательную, P в 2 раза меньше.
Пример. Разность между средними равна 6,6 г, повторность семикратная, ошибка разности 2,1 г, следовательно,
t = 6,6/2,1 = 3,14.
При n = 7 по табл. 14 имеем Р=2%,т. е. в2% всех случаев разность выходит за пределы ± 6,6 г. Исчезновение положительной разности между средними, т. е. отклонение за пределы разности 6,6 г, равно Р/2 = 2%/2 = 1 %, или одному случаю из 100 возможный
В практике оценки результатов опытов установилась привычка брать для оценки достоверности разности двойную или тройную ошибку, не учитывая числа наблюдений, на основе которых выведена ошибка опыта. Из разобранных примеров видно, насколько последнее может иногда привести к неверным суждениям о достоверности результатов опыта.
Метод А.А. Сапегина. В практике сельскохозяйственного опытного дела широкое применение при обработке результатов полевого опыта имел у нас метод приведения А.А. Сапегина. Особенностью этого метода является то, что обрабатываются процентные отклонения от средних арифметических по вариантам. В основе его лежит предположение, что величина ошибки опыта пропорциональна величине урожаев. Экспериментальные данные не подтвердили этого предположения, но метод А.А. Сапегина дает в конце обработки очень удобную для оценки точности опыта процентную ошибку среднего (т. е. m), выраженную в процентах от среднего урожая для опыта: P = 100 m/М. Этот показатель относительной точности исследования весьма удобен для сравнения различных опытов по степени их точности. G этой целью может быть применено вычисление ошибки среднего, выраженной в процентах от среднего урожая для всего опыта в целом: m*100/M опыта.
Метод анализа вариации Р.А. Фишера. Статистическая обработка результатов полевых опытов при наличии в опытах систематической ошибки, вызываемой неравенством исходного плодородия почвы, весьма сложна. Для устранения систематической ошибки полеводы применяют не только различные приемы статистической обработки результатов полевого опыта, но и различные приемы размещения в поле опытных делянок, что, в свою очередь, накладывает свой отпечаток на приемы статистической обработки результатов. Постановка полевых опытов с большим числом вариантов в условиях изменчивого плодородия почвы — весьма сложная методическая задача, различно решаемая в многочисленных работах полеводов-опытников и математиков. Мы здесь даем анализ точности простого полевого опыта, имеющего небольшое число вариантов и поставленного на достаточно выровненном по плодородию участке.
Кроме установления точности опыта и степени достоверности наших суждений, обработка результатов опыта помогает определить пригодность его для решения поставленной задачи. Пригодность опыта определяется прежде всего правильностью составления схемы опыта и выбором надлежащих условий для его проведения. Достоверность разности между контрольными вариантами и служит одним из показателей пригодности опыта для решения данной задачи. Например, если опыт ставится с целью определения эффективности различных новых форм азота, то контрольными вариантами в опыте являются варианты без азота и с внесением стандартного азотного удобрения. Если между этими вариантами имеется достоверная разность, опыт пригоден для решения поставленной задачи, если нет, то результаты опыта не могут быть использованы. Если в условиях опыта растения вообще не нуждались в азоте, то изучать в этих условиях эффективность новых азотных удобрений не следует. Таким образом, пригодность опыта (его репрезентативность) определяется путем вычисления D/mD для контрольных вариантов схемы опыта.
В практике Ротамстедской сельскохозяйственной опытной станции в Англии и отчасти на опытных станциях США получил распространение метод, разработанный Р.А. Фишером и названный им анализом вариации (рассеяния, дисперсии). В практике сельскохозяйственного опытного дела России этот метод, несмотря на проявленный к нему в свое время большой интерес, не получил большого распространения.
При обработке результатов опыта по методу анализа вариации (рассеяния) сначала находят средний урожай в опыте, затем вычисляют отклонения от него всех урожаев отдельных делянок. Эти отклонения возводят в квадрат и находят их сумму, которая соответствует общей вариации (рассеянию) опыта. Далее вычисляют средние урожаи для вариантов, их отклонения от среднего урожая, квадраты отклонений и их сумму. Последнюю умножают на число повторений. Полученная величина характеризует изменение урожаев в зависимости от вариантов. Затем определяют средние урожаи по повторениям, их отклонения от среднего урожая для опыта, квадраты этих отклонений и их сумму, которая после умножения на число вариантов дает величину, характеризующую варьирование урожаев, вызываемое различным плодородием повторений. Вычитая из суммы квадратов, характеризующей общее рассеяние в опыте, величины, найденные для рассеяния вариантов и повторений, находят величину суммы квадратов, соответствующую случайным отклонениям, или остаточное рассеяние (вариацию) в опыте.
Вычисление величин, характеризующих рассеяние общее, вариантов повторений и случайное, может идти с использованием квадратов не отклонений, а квадратов величин урожаев по делянкам, по повторениям и по вариантам, но это целесообразно только при наличии счетных машин.
Полученные суммы квадратов следует соответственно разделить на число степеней свободы для вариантов на (l—1) и для повторений на (n—1) и для случайного рассеяния на (n—1)*(l—1). После деления сумм квадратов на число степеней свободы получаем средние квадраты.
Отношение среднего квадрата вариантов к среднему квадрату случайного рассеяния и является критерием точности опыта и его пригодности для решения поставленного вопроса. При этом используются таблицы Снедекора, в которых указывается, при каком отношении средних квадратов изменение урожаев, вызываемое вариантами, имеет вероятность в 95 или 99% (см. табл. 20 и 21).
Пример использования анализа вариации приведен далее при обработке результатов полевого опыта.
При работе методом анализа вариации данные для всего опыта обрабатывают совместно, так как этот метод такой же обобщенный, как и описанный ранее. Далее, и в том и в другом методе при анализе вариации все вычисления производят с абсолютными величинами отклонений. В результате вычислений оба метода дают одну и ту же величину суммы квадратов случайных отклонений; только в одном случае они определяются непосредственно, а при анализе вариации — по разности. Исключение влияния изменения плодородия почвы по повторениям опыта в том и другом случае производится на основе одного и того же принципа.
Существенное различие между обоими методами заключается в том, что в одном случае устанавливается ошибка опыта, т. е. ошибка разности между двумя средними, а в другом — критерий Фишера, характеризующий, во сколько раз отклонения между вариантами больше случайных.
В основе этого метода лежит предположение, что опыт в том случае пригоден, когда различие между вариантами опыта больше, чем между урожаями параллельных делянок или сосудов. Если изменения в урожаях по делянкам, вызываемые случайными, неучитываемыми причинами, больше, чем изменения, вызываемые изучаемыми факторами, опыт считается непригодным для установления действия последних на урожай растений.
При обычной оценке достоверности опыта устанавливают, во сколько раз разность между средними для двух вариантов опыта превышает ее ошибку. Ho в одном и том же опыте разности между различными парами средних обладают различной степенью достоверности в зависимости от величины разности. Критерий, предложенный Фишером, является попыткой однозначно характеризовать достоверность действия изучаемых факторов для всего опыта в целом.
Средние арифметические для вариантов опыта образуют ряд цифр, который характеризует действие изучаемых в опыте факторов. Установив для этого ряда цифр его квадратическое отклонение, мы можем сравнить его с квадратическим отклонением, характеризующим действие в опыте случайных причин. Так как на изменении ряда средних по вариантам сказываются и случайные причины, то, если изучаемые факторы существенно сказались на высоте урожаев, квадратическое отклонение для средних по вариантам должно быть достоверно больше, чем квадратическое отклонение, характеризующее действие случайных, неучтенных причин. Ho в некоторых случаях применение критерия Фишера не дает правильных результатов, так как он учитывает изменчивость между всеми вариантами опыта, тогда как для определения пригодности опыта необходимо учитывать различие только между определенными контрольными вариантами опыта. При постановке опыта все варианты схемы опыта можно разбить на два вида: контрольные, которые показывают чувствительность в опыте растений к изучаемому фактору, и испытуемые. Между последними может и не быть никакого расхождения, в результате чего уменьшится основное отклонение изменчивости по вариантам при наличии в опыте сильного действия изучаемого фактора. Например, изучая различные формы новых растворимых фосфатов, мы, имея опыт с громадной чувствительностью растений к количеству усвояемой P2O5, можем получить малую изменчивость между вариантами опыта, если число одинаково усвояемых форм будет велико.
Для анализа достоверности опыта и его пригодности мы предлагаем определять достоверность разницы между контрольными вариантами опыта. Под последними следует при этом понимать не только делянки без удобрений, но и все делянки опыта, при помощи которых устанавливается чувствительность опытных растений к изучаемому фактору. В зависимости от задач опыта эти контрольные варианты будут различными.
В практике опытного дела в России анализ вариации (рассеяния, дисперсии) используют как способ вычисления ошибки опыта, без применения критерия Фишера. Этот способ вычисления сложнее и менее удобен, чем вычисления ошибки опыта с исправлением отклонений по повторениям, хотя и дает те же результаты.
Пример обработки результатов полевого опытаВ целях освоения наиболее простых практических приемов обработки результатов полевого опыта рассмотрим детально обработку результатов одного опыта.
В 1955 г. Центральной станцией удобрений и агропочвоведения СоюзНИХИ был проведен полевой опыт с внесением фосфорных удобрений в подкормку под хлопчатник. Опыт был поставлен на общем для всех делянок опыта фоне удобрений, который состоял из 40 кг P2O5, внесенных в виде суперфосфата до посева, и 110 кг азота, внесенного в подкормку в виде аммиачной селитры. В схеме опыта всего было 8 вариантов (l=8):
1. Одно фоновое удобрение («фон»).
2. Фон + суперфосфат из апатита.
3. Фон + суперфосфат из каратауского фосфорита.
4. Фон + аммонизированный суперфосфат.
5. Фон + аммофос ив каратауского фосфорита.
6. Фон + аммофос из апатита.
7. Фон + плавленый магниевый фосфат.
8. Фон + обесфторенный фосфат.
Фосфорные удобрения вносились в подкормку в дозе 40 кг P2O5; при внесении аммофоса количество азота в фоновом удобрении соответственно уменьшалось на содержание азота в аммофосе. Опыт был поставлен в четырехкратной повторности (n = 4). Задача математической обработки результатов этого опыта установить: было ли в опыте вообще достоверное положительное действие фосфатов и если оно было, то были ли в опыте достоверные различия между эффективностью различных форм фосфорных удобрений, внесенных в подкормку.
Прежде всего необходимо составить таблицу данных опыта, по которой можно удобно подсчитать средние урожаи по вариантам и по повторениям опыта (табл. 15). Составив эту таблицу и подсчитав сумму урожаев для каждого варианта и каждого повторения, находим затем общую массу урожаев, полученных со всех 32 делянок опыта (1191,8). Складывая урожаи по вариантам или складывая урожаи по повторениям, получаем ту же величину, что свидетельствует о правильности наших подсчетов. Затем вычисляем средние урожаи для каждого варианта и для каждого повторения. При этом средние урожаи по вариантам мы записываем с точностью до 0,1 ц/га.
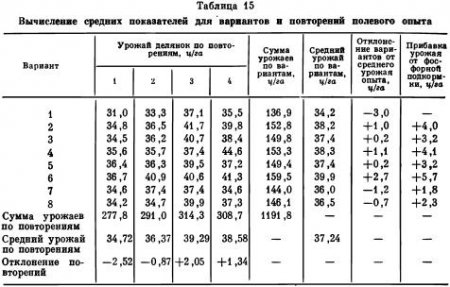
Цель опыта — установить прибавки урожаев хлопчатника от внесения в подкормку фосфорных удобрений, а задача математической обработки результатов опыта — установить степень их достоверности. Вычитая из величин средних урожаев по вариантам опыта (с 2-го по 7-й) величину среднего урожая flo первому варианту (фон), получим прибавки урожаев хлопка-сырца (в ц/га) от внесения фосфатов. Эти прибавки колеблются в зависимости от формы фосфорного удобрения от 1,8 до 5,7 ц/га хлопка сырца (см. табл. 15).
Разделив общую сумму урожаев на число делянок в опыте, получим средний урожай в опыте: 1191,8 : 32 = 37,24. Разделив суммы урожаев по повторениям на число вариантов, находим средние урожаи по повторениям. Вычитая из них величину среднего урожая для опыта, получаем отклонения для урожаев по повторениям; они равны — 2,52: -0,87; + 2,05 и + 1,34. Как видим, первое повторение дает более низкие урожаи, а третье — более высокие, чем остальные повторения. Видимо, в опыте имело место изменение плодородия почвы при переходе от одного повторения к другому. Следовательно, при обработке результатов опыта надо исключить влияние варьирования величин урожаев по повторениям. Это достигается двумя способами: во-первых, путем получения исправленных отклонений для каждой делянки и, во-вторых, путем вычитания суммы квадратов отклонений по повторениям, умноженной на число вариантов из суммы квадратов неисправленных отклонений.
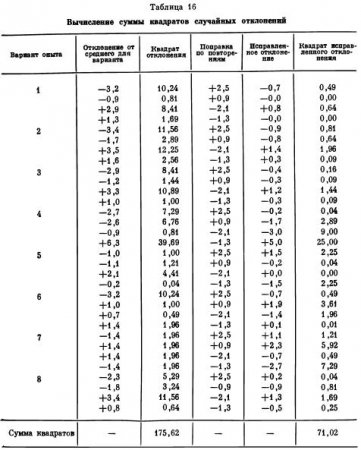
Остановимся сначала на первом способе с использованием исправленных отклонений. С этой целью устанавливаем поправки по повторениям, они будут равны отклонениям повторений, взятым с обратным знаком, +2,5, +0,9, — 2,1 и — 1,3. Вычисление ошибок опыта производим на основе отклонений величин урожаев отдельных делянок от среднего по варианту. Эти отклонения приведены в графе 2 табл. 16. Например, для 1-го варианта, согласно табл. 15, имеем урожаи: 31,0; 33,3; 37,1; 35,5; средний урожай по варианту равен 34,2. Тогда отклонения равны: 31,0-34,2 = -3,2; 33,3-34,2 = - 0,9 и т.д. (см. табл. 16). Эти отклонения исправлены во всех вариантах на величину поправок по повторениям, указанным в графе 4 табл. 16, в графе 5 приведены исправленные отклонения, а в графе 6 — квадраты этих отклонений. Сумма всех этих квадратов равна 71,02, ее мы должны разделить на число степеней свободы. Общее число делянок в опыте 32, следовательно, общее число степеней свободы в опыте равно 32—1 = 31, число степеней свободы для вариантов равно 8—1 = 7 и для повторений 4—1 = 3. При вычислении исправленных отклонений мы уже исключили влияние повторений, а вычисляя отклонения внутри вариантов, исключили влияние вариантов. Таким образом, на долю случайного (остаточного) варьирования осталась 31—7—3 = 21 степень свободы. Эту же величину средней свободы находим, умножив число степеней свободы вариантов на число степеней свободы повторений (l—1 = 8—1 = 7 и n—1 = 4—1= 3). Вычисление квадратичного отклонения производим по формуле
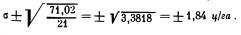
Следовательно, ошибка среднего по вариантам равна:
Ошибка разности двух средних равна:
Рассмотрим второй способ вычисления ошибки опыта. Возведем в квадрат неисправленные отклонения урожаев делянок от средних по вариантам (графа 3, табл. 16) и найдем их сумму 175,62. Возведем в квадрат отклонения по повторениям и найдем их сумку (табл. 17), которая будет равна 13,11. Эта сумма квадратов характеризует варьирование в зависимости от повторений в пределах одного варианта. Общее число вариантов равно 8; умножив на него сумму квадратов отклонений (∑v2) 13,11, получим ∑ (∑v2) = 13,11*8 = 104,88, т. е. величину, характеризующую влияние различного плодородия повторений на варьирование урожаев в опыте.

Вычитая из суммы квадратов неисправленных отклонений ∑(∑v2) = 175,62 варьирование повторений 104,88, получаем величину варьирования исправленных отклонений 70,74. Она только на 0,28 меньше, чем найденная первым способом (71,02); расхождение вполне понятное, так как при вычислении мы прибегали к округлению цифр до 0,1 или 0,01. Вычисление по второму способу дает те же величины, что и по первому: σ = ± 1,84, m = ± 0,92 и mD = ± 1,30.
Если бы не учли изменения плодородия почвы по повторениям и в основу наших вычислений положили бы сумму квадратов неисправленных отклонений, то величина квадратичного отклонения была бы равна + 2,70 и т = +1, 35, так как
В результате мы получили бы неправильное представление о малой точности опыта. Достоверность прибавок урожаев в опыте определяется тем, во сколько раз они превосходят свою ошибку. Вычисление ошибки разности (mD) производим при использовании 21 степени свободы; по табл. 14 находим, что для 20 степеней свободы 5% показаний будет находиться за пределами ± 2,09 mD, 1% показаний — за пределами ±2,84 mD.
Следовательно, прибавки урожаев, полученные в опыте, в 95% случаев будут отклоняться от найденных средних не более как на ± 2,09 mD = ± 2,09*1,30 = ± 2,7 ц, а в 99% случаев не более как на ± 2,84*1,30 = 3,7 ц. Ho в данном случае нас интересует не столько возможность получения прибавок определенного размера, сколько достоверность наличия разности между вариантами. В этом случае важно учесть возможный процент вероятных отклонений за пределы не ± mD, а только за пределы — mD. Последний будет вдвое меньше указанного в табл. 14 для ± mD, поэтому берем для характеристики вероятной ошибки в размере 5% случаев — 1,73 mD, а для 1% — 2,53 mD, т. е. для нашего опыта имеем соответственно 2,3 и 3,3 ц.
Большинство прибавок урожая от внесения фосфорных удобрений, кроме прибавок, полученных в 7-м и 8-м вариантах, больше 2,3 ц, следовательно, заслуживают внимания; более достоверными следует считать, однако, те прибавки, которые больше 3,3 ц.
Рассматривая внимательно данные табл. 15, видим, что урожай по одной из делянок, именно в четвертом варианте четвертого повторения, исключительно высок и равен 44,6 ц. Этот урожай превышает урожай среднего для этого варианта на 6,3 ц/га.
Основное отклонение в опыте было равно + 1,84¾, следовательно, отклонение этой делянки от среднего превышает основное отклонение в 3,4 раза. Среднее для трех других повторений этого варианта равно 36,2 ц, т. е. на 8,4 ц меньше, чем урожай в четвертом повторении. Такое отклонение от средних бывает весьма редко, меньше чем 1 раз в 1000 случаев, и наличие его дает неправильное представление об эффективности четвертого варианта. Целесообразно поэтому провести обработку данных опыта, исключив эту делянку.
Обработка опыта при отсутствии одной делянки может быть сделана для оставшихся вариантов, имеющих нормальное число повторений; обработка может быть сделана и для всех повторений, за исключением повторения с забракованной делянкой. Можно также сохранить обработку данных опыта в целом.
Исключив делянку с урожаем в 44,6 ц, мы уменьшаем общий урожай всех делянок до 1147,2 ц, средний урожай в опыте становится равным 37,0 ц, поправки на плодородие повторений опыта тоже меняются. Они становятся равными + 2,3, + 0,6, — 2,3 и — 0,7. При вычислении их можно исходить из среднего урожая для 8 вариантов первых трех повторений и 7 вариантов четвертого повторения, так как урожаи последнего варианта несущественно отличаются от урожаев других вариантов. В противном случае пришлось бы вычислять поправку по повторениям и средний урожай в опыте, исключив все делянки дефектного варианта.
Произведя заново вычисления исправленных отклонений и их квадратов, находим сумму квадратов отклонений ∑v2 = 34,11 при 20 степенях свободы. Квадратическое отклонение δ уменьшилось до 1,32 ц, ошибка среднего m для варианта стала 0,66 ц и ошибка разности mD средних вариантов ± 0,93 ц. Ho эта ошибка разности средних не применима в тех случаях, когда в сравнении участвует четвертый вариант, в котором только три повторения. Ошибка разности в этом случае будет равна 1,01 ц. Так как для четвертого 1,32 варианта m = ± 1,32/√3 = ± 0,76, то, следовательно,
Считая, что существенное различие (вероятное в 95% всех случаев) между разностями равно 1,73*mD, имеем 1,73*0,93 = 1,6 ц и 1,73*1,01 = 1,75, т. е. все прибавки урожаев в нашем опыте заслуживают внимания, а действие подкормки аммофосом сильнее, чем другими фосфорными удобрениями.
В большинстве опытов особое значение имеют фоновые, или контрольные, делянки, с которыми сравниваются урожаи прочих вариантов опыта. Если хотя бы одна из этих делянок окажется почему-либо поврежденной, то точность наших выводов существенно уменьшится. Поэтому весьма важно иметь в опыте удвоенное количество фоновых (контрольных) делянок, т. е. иметь для фона два тождественных варианта. При вычислении ошибки опыта они участвуют как отдельные самостоятельные варианты.
Ho при вычислении прибавки урожаев против фона (контроля) используется уже средний урожай для всех фоновых делянок. В этом случае ошибка фонового варианта меньше, чем ошибка прочих вариантов. Ошибка прибавок урожая против фона равна
вместо mD = ± 1,41 m, когда сравниваются другие варианты. Увеличение числа контрольных (или фоновых) делянок не только гарантирует сохранность опыта, но и повышает точность основных выводов.
Приведенный способ обработки при помощи вычисления отклонений имеет преимущество большой наглядности: исследователь видит, что именно определяет точность его работы и какие отдельные урожайные данные сомнительны и какие средние величины заслуживают поэтому меньшего доверия. Так, средние для вариантов, в основе которых лежат сильно расходящиеся показания, должны быть оговорены, для таких вариантов приводятся средние как из всех повторений, так и из меньшего числа повторений, не вызывающих сомнений. Браковка делянок, дающих сильно отклоняющиеся показания (> 3 δ), специально оговаривается при опубликовании данных опыта.
Приведенный нами способ обработки результатов опыта позволяет использовать и метод анализа вариации Фишера. Для этого необходимо вычислить средний квадрат рассеяния (вариации) вариантов опыта. Вычисляем отклонения урожаев по вариантам от среднего урожая в опыте, возводим их в квадрат, определяем сумму квадратов и умножаем ее на число повторений (табл. 18). Получаем, что ∑ (∑v2) для вариантов равна 20,51*4 = 82,04. Теперь легко можно составить таблицу анализа вариации в опыте по Фишеру (табл. 19), так как остальные необходимые величины уже были нами вычислены ранее. Чтобы установить пригодность опыта для решения поставленного вопроса, мы должны установить отношение среднего квадрата вариантов к среднему квадрату случайного отклонения; оно равно 11,72 : 3,37 = 3,48.
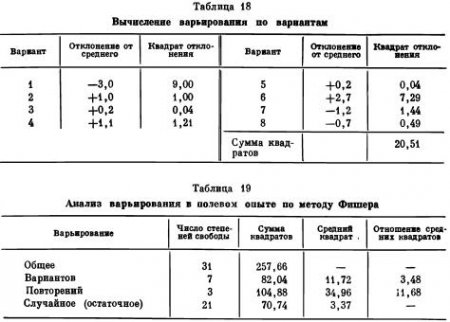
Обратимся к данным табл. 20, учтя поправочную таблицу Снедекора. При наличии 21 степени свободы (7 — для вариантов и 3 — для повторений) для вероятности в 95% отношение между средними квадратами по таблице Снедекора должно быть не меньше 2,50; наше отношение равно 3,48. Для вероятности в 99% (табл. 21) находим, что соотношение между средними квадратами при указанных степенях свободы, по Снедекору, должно быть не меньше 3,65; наше же отношение только немного меньше его — 3,48. Следовательно, можно считать опыт вполне пригодным для решения вопроса, который в ней изучался.
Повторения опыта тоже существенно различались по своему плодородию. Отношение среднего квадрата для повторений к среднему квадрату случайного рассеяния при вероятности в 95% равно 39,96 : 3,37 = 11,68. По таблице Снедекора для большей вероятности (в 99%) отношение должно быть в этом случае не менее 5,78; в нашем опыте оно много больше — 11,68.
В практике опытного дела обработку результатов опыта часто ведут специальные отделы статистики. Это обеспечивает качество обработки. Ho исследователь должен сам хорошо понимать, в силу каких особенностей опыта получилась та или иная степень его точности, что собственно характеризует полученные показатели и как их следует применять с различными целями. Это возможно только тогда, когда ему ясен весь ход обработки данных его опыта.