Вычисление и использование коэффициентов корреляции и регрессии и установления их ошибок
На Мироновской сельскохозяйственной опытной станции с различных делянок многолетних опытов были взяты образцы почвы северного малогумусного мощного чернозема. На этих образцах были поставлены вегетационные опыты с внесением в почву радиоактивной метки для определения запасов в почвах усвояемых для растений фосфатов. Эти же почвенные образцы были проанализированы по методу Труога для определения содержания в них легкорастворимых, или подвижных, фосфатов.
В результате получилось два ряда показаний, характеризующих взятые почвенные образцы: запасов в них усвояемых фосфатов и содержания в них фосфатов, растворимых по методу Труога. Спрашивается, можно ли на основании анализов почвы по методу Труога судить о содержании в почвах усвояемых для растений фосфатов?
Для ответа на этот вопрос надо определить коэффициент корреляции, который в данном случае показывает степень сопряженности показаний химического анализа почв и результатов вегетационных опытов, поставленных на тех же образцах почвы.
В табл. 22 приведены результаты анализов и вегетационных опытов, а также порядок вычисления коэффициента корреляции.
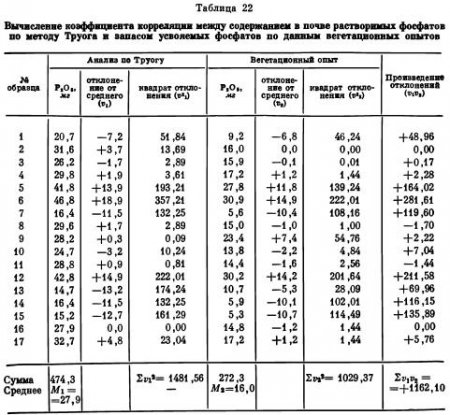
Содержание в почве растворимых фосфатов было значительно больше, чем усвояемых: в среднем в образцах почвы было найдено 27,9 мг P2O5 по данным химического анализа и только 16,0 мг P2O5 по данным вегетационных опытов. Ho, просматривая оба ряда цифр, видим, что они меняются соответственно один другому. Для вычисления коэффициента корреляции определяем для каждого ряда отклонения отдельных показаний от их средних величин. В большинстве случаев положительное отклонение в одном ряду совпадает с положительным отклонением в другом ряду. Поэтому и произведения отклонений в большинстве случаев — положительные величины. Произведения отклонений, положительные и отрицательные, складываем и определяем их сумму ∑v1v2, в данном случае она равна 1162,10. Отклонения отдельных показаний от соответственных средних величин 27,9 для химических анализов и 16,0 для результатов вегетационных опытов возводим в квадрат и суммируем квадраты отклонений, в результате получаем: ∑v1в2 = 1481,56 и ∑v2в2 = 1029,37.
Следовательно, коэффициент корреляции между показаниями химических анализов и результатами вегетационных опытов будет равен:
Пользуясь таблицами Барлоу, легко производим вычисление необходимых квадратов и квадратных корней.
Вычисление ошибки коэффициента корреляции, т. е. его стандартного, или квадратического, отклонения от возможного истинного значения коэффициента корреляции, производим в данном случае по формуле, предложенной Фишером для небольшого количества пар сравниваемых величин
где n — количество пар сравнений, в данном случае 17.
Это количество уменьшается на 2, так как для получения коэффициента корреляции используются две средние величины для двух рядов; следовательно, число степеней свободы уменьшается на 2. Подставляя полученные нами величины в формулу Фишера, имеем
Таким образом, в результате вычислений:
r = + 0,941 ±0,087.
Для оценки степени достоверности или существенности, т. е. определения того, в каком количестве возможных случаев корреляция между двумя рядами будет вообще иметь место, определяем величину t, т. е. отношение величины коэффициента корреляции к его ошибке:
Пользуясь далее табл. 14, видим, что в данном случае наличие корреляции доказано более чем для 99,75% возможных случаев. При этом пользовании табл. 14 в данном случае вместо величины n—1 берется n—2.
Ошибка коэффициента корреляции, как это видно из его формулы, зависит от двух величин: числа степеней свободы, т. е. количества пар сравнений, уменьшенного на 2, и от величины самого коэффициента корреляции. Вполне понятно, что наличие соответствия между двумя величинами тем достовернее, чем более тесно связано изменение величин одного ряда с изменением показаний другого ряда и чем больше пар сравнений имеется для выявления этого соответствия. Для принятого при биологических исследованиях установления вероятности определений в 95 и 99 % (или «существенности на уровне 5 и 1%») составлена табл. 23, по которой на основе величины r и n — 2 определяют степень достоверности коэффициента корреляции.
Эту таблицу приводим из руководства Снедекора.
В нашем примере найденный коэффициент корреляции и степень его достоверности определенно говорят о том, что между содержанием в почве растворимых фосфатов по Tpyory и количеством в почве усвояемых для растений фосфатов имеется корреляция или даже определенная причинная зависимость, конечно, для конкретных условий проведения опытов.
Поэтому вполне целесообразно и установление коэффициента регрессии (b) количества усвояемых фосфатов в почве по содержанию в ней растворимых фосфатов:
Таким образом, если содержание в почве растворимых фосфатов меняется на 1 мг P2O5, содержание усвояемых фосфатов в ней меняется на 0,784 мг P2O5. Следовательно, на основе отдельных показаний для растворимых фосфатов (x) можем вычислить количество в почве усвояемых для растений фосфатов (у) по уравнению
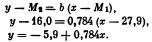
Предположим, что анализ установил содержание в почве в одном случае 41,8 мг P2O5 и в другом 32,7 мг P2O5. Тогда по приведенной формуле находим запасы усвояемых фосфатов в почве; они будут соответственно равны 26,8 мг P2O5 и 19,7 мг P2O5. В вегетационных опытах (см. табл. 22, показания для образцов 5 и 17) были получены соответственно следующие величины: 27,8 мг P2O5 и 17,2 мг P2O5. Таким образом, отклонения величин, вычисленных по формуле регрессии, от величин экспериментально найденных было — 1,0 мг и + 2,5 мг. Такое расхождение между данными, полученными на основе химического анализа и результатами опытов, нельзя считать значительным. Конечно, такое расхождение между данными двух химических анализов было бы недопустимым.
Для установления возможной степени достоверности коэффициента регрессии определим его основное квадратическое отклонение по формуле
где ∑d2 — сумма квадратов отклонений экспериментально найденных величин от величин, вычисленных по формуле регрессии.
Эта сумма квадратов может быть найдена двумя путями: во-первых, путем непосредственного определения отклонений найденных величин от вычисленных для всех образцов почвы, последующего возведения их в квадрат и нахождения их суммы (см. табл. 24); во-вторых, путем использования следующей формулы:
Подставляя в эту формулу соответствующие величины из табл. 22, имеем:
Отсюда вычисляем основное квадратическое отклонение для расхождений между вычисленными и найденными величинами:
Таким образом, отклонение найденных в опытах величин от вычисленных по формуле регрессии может быть весьма существенным, хотя ошибка вычисления коэффициента регрессии и невелика, она равна
Тот же результат получаем и при вычислении ошибки коэффициента регрессии по табл. 24. В результате округления количества усвояемых фосфатов (вычисляемых по формуле) до 0,1 мг сумма квадратов отклонений ∑d2 несколько (на 0,21) отличается от вычисленной ранее, но это, конечно, не отражается на результатах определения ошибки коэффициента регрессии.
Величина t, т. е. отношение коэффициента регрессии к его ошибке b/mb,
та же, что и для коэффициента корреляции. Для оценки достоверности коэффициента регрессии или степени его существенности можем использовать табл. 14 так же, как это ранее делали для коэффициента корреляции. Несмотря на высокую степень точности вычисления коэффициента регрессии в нашем примере, отдельные показания, полученные в опытах, могут существенно отличаться от вычисленных на основе формулы регрессии. Из данных табл. 24 видно, что расхождения между экспериментально найденными и вычисленными величинами достигали 5,1 и 7,2 мг P2O5, т. е. были равны 32 и 45% от средней величины.
В нашем примере тройное квадратическое отклонение
3σ = 2,80*3 = 8,40 мг Р2О5,
следовательно, получение таких больших расхождений, как 5,1 и 7,2, возможно.
При анализе опытных данных, когда мы хотим установить соответствие между двумя рядами показаний, необходимо прежде всего установить коэффициент корреляции и степень его достоверности.
Вполне возможно, что коэффициент корреляции будет установлен с большой достоверностью, но величина его будет малой. Тогда не имеет смысла вычислять коэффициенты регрессии, так как, видимо, оба ряда сравниваемых явлений подчиняются разным закономерностям. Если между этими рядами имеется высокая и достоверная корреляция, то вычисление коэффициента регрессии поможет нам более полно осветить наблюдающиеся явления. Например, предположим, что для ряда образцов почвы были проведены определения содержания в почве подвижных форм калия двумя методами: более сложным и дорогим стандартным методом и более простым и дешевым новым методом. Между показаниями этих методов найдена высокая и достоверная корреляция. Тогда, вычисляя коэффициент регрессии для нового метода, можем, работая новым методом, перечислять его показания в показания стандартного метода, для которых уже установлены соответствующие градации отзывчивости почв на внесение калийных удобрений. Ho достаточно ли наличие высокого коэффициента корреляции и точно определенного коэффициента регрессии, чтобы обоснованно рекомендовать замену стандартного метода новым методом? Предположим, что почвы по степени обеспеченности их калием разбиты на группы, различающиеся на 5 мг калия, а основное квадратическое отклонение между найденными показаниями и вычисленными по формуле регрессии равно 1 мг калия. Тогда большое количество образцов почв, отнесенное при работе стандартным методом в одну группу по степени обеспеченности почв калием, попадет в другую группу, если мы будем работать новым методом, несмотря на высокую корреляцию между показаниями этих методов и точно установленный коэффициент регрессии. Для большинства агрономических явлений поэтому важно определение основного квадратического отклонения для расхождений между данными, полученными в опыте и вычисленными по формуле регрессии.
Коэффициент корреляции показывает, насколько варьирование одного ряда показаний происходит согласованно с изменением показаний для другого ряда. Общая же изменчивость показаний для каждого ряда характеризуется суммой квадратов отклонений отдельных показаний от среднего, т. е. ∑v2. Квадрат коэффициента корреляции r2 показывает долю участия в общем варьировании (∑v2) согласованных изменений двух рядов, а (1—r2) является остаточной частью варьирования, т. е. долей несогласованных изменений.
Для наглядной характеристики степени корреляции двух рядов часто необходимо указывать не только величину r, но и r2 или 1—r2. Это имеет значение при характеристике корреляции между высотой урожаев и количеством применяемых удобрений, при бонитировке почв по данным анализов или высоте урожаев и других агрономических вопросов. Например, при решении вопроса о замене одного метода анализа почв на содержание подвижных питательных элементов другим коэффициент корреляции, равный + 0,9 (высокий при решении многих биологических вопросов), соответствует большому количеству несогласованных изменений в показаниях методов, так как в этом случае 1—r2 = 1—0,81 = 0,19. Следовательно, количество несогласованных изменений в показаниях составляет 19%.